私鑰分割 - Shamir's Secret Sharing
在做區塊鏈應用的時候,最常碰到的一個問題就是,怎麼保管私鑰,怎麼讓使用者方便,但又同時是安全的。第一個想法就是備份金鑰(不論是passphrase/keystore/私鑰),但是如果把使用者金鑰(加密)備份到自己的server,只要server的安全上有個不小心,使用者的金鑰就可能就被盜取了,就算是加密過的,也難保不會被破解。那如果切成好幾部分,有好幾份備份呢? 那怎麼切,才能確保安全呢?這就是本篇的重點啦!
最直覺的想法就是直接切成N等份,例如32bytes的私鑰分成四份,然後任三份可以組成完整的私鑰,這樣每份至少需要11 bytes。聽起來問題好像解決了,但要怎麼切分,可以保證4取3可以完整組回私鑰,又是另一個麻煩的問題(自己寫的演算法,如果沒有被完整測試過,屆時使用者的私鑰組不回來,公司的問題就大了)。ZeroPass有作切分金鑰並且提供備份的服務,不過找不到他們背後的演算法,後來google到Shamir's Secret Sharing,覺得很酷,在概念上用很簡單的數學就解決了這個問題,所以在這裡跟大家分享。
我是參考這篇,淺顯易懂,不介意看英文的可以直接看。
如何拆分
先定義一下要我們接下來要幹嘛
1. 把秘密(secret)拆分成N份,並且只需M(M < N)份即可組回完整的秘密,被拆分過的每一份秘密叫做share
2. 建立一個(M-1)次方程式
假設,我們要傳遞的秘密是數字3,然後希望3份(M=3)就能回復完整的秘密,所以要建立一個一元二次(M-1)方程式,y=ax2+bx+c。
a跟b可以任選,而c是秘密(在我們的例子就是3),我們選a=2, b=1,所以方程式為y=2x2+x+3。
方程式圖如下:
接著,我們任意取三點(因為M=3),(1, 6),(2, 13),(-2, 9)
而這三個點座標就是三個share。最終可以由這三個點座標(share)還原秘密(secret)。
如何還原
目標是,還原(M-1)次方程式。若取得原本的方程式,即可拿到原本的秘密。我們知道兩點可以成一直線,而三點可以定義一個拋物線。現在,我們有三個點(1, 6),(2, 13),(-2, 9),但不知道曲線
不過M=3,所以可以知道方程式為y=ax2+bx+c,然後,我們知道三個座標(1, 6),(2, 13),(-2, 9),接著就是國中數學了
(1, 6) ==> c = a + b -6
(2 13) ==> c = 4a + 2b -13
(-2, 9) ==> c = 4a - 2b - 9
過程就不推導了,最後就可以得出a=2, b=1然後我們的秘密數字c=3。是不是很神奇啊!
不過在實際上,會使用Lagrange polynomial(多項式的插值方法)做secret的計算,多項式如下(直接截wiki的圖)
我們目前已知三點
f(1) = 6
f(2) = 13
f(-2) = 9
帶入上述多項式,可得
f(1) = 6
f(2) = 13
f(-2) = 9
帶入上述多項式,可得
最後得到一樣的方程式2x²+x+3。
在Shamir Secret Sharing中,需要選定一質數P,而Secret需要小於質數。所以最後方程式得出的值需要再對質數P取餘數。
Shamir's Secret Share in Java
Shamir's Secret Sharing in C
謝謝@Chang-Wu Chen針對secret計算的指正。




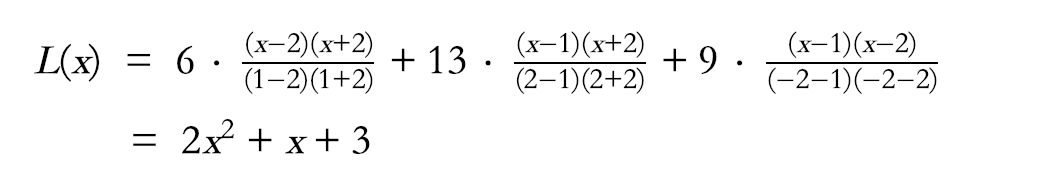


留言
張貼留言